What is Backpropagation?

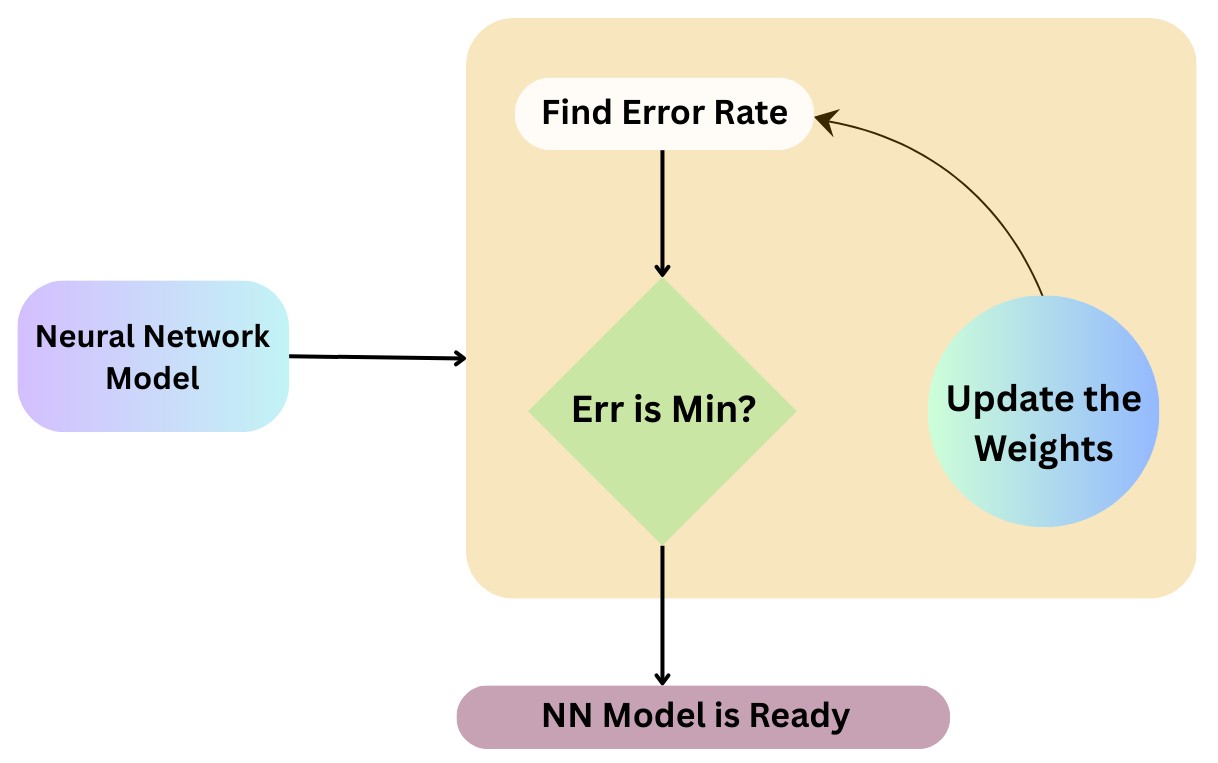
Backpropagation is a core algorithm used to train neural networks. Short for “backward propagation of errors,” it’s a mathematical technique that fine-tunes the internal parameters, weights, and biases of a neural network by minimizing the gap between the predicted output and the actual expected result (often called the target or ground truth). The process is iterative, adjusting the model step-by-step to make it more accurate over time.

At its core, backpropagation is about making the network better with each step by figuring out how each part should adjust to reduce future errors.

It is done by calculating how much each parameter in the network contributed to the final error, then tweaking those values in the right direction. Over many cycles of prediction and correction, the network learns to make better decisions.

Backpropagation dates back to the 1960s, but it became practical in 1986 when Rumelhart, Hinton, and Williams showed it could efficiently train deep networks. Before that, training was unreliable as models struggled to learn internal patterns without manual feature design. Backpropagation solved this by enabling networks to adjust their internal layers automatically, laying the groundwork for modern deep learning.

What is Neural Network

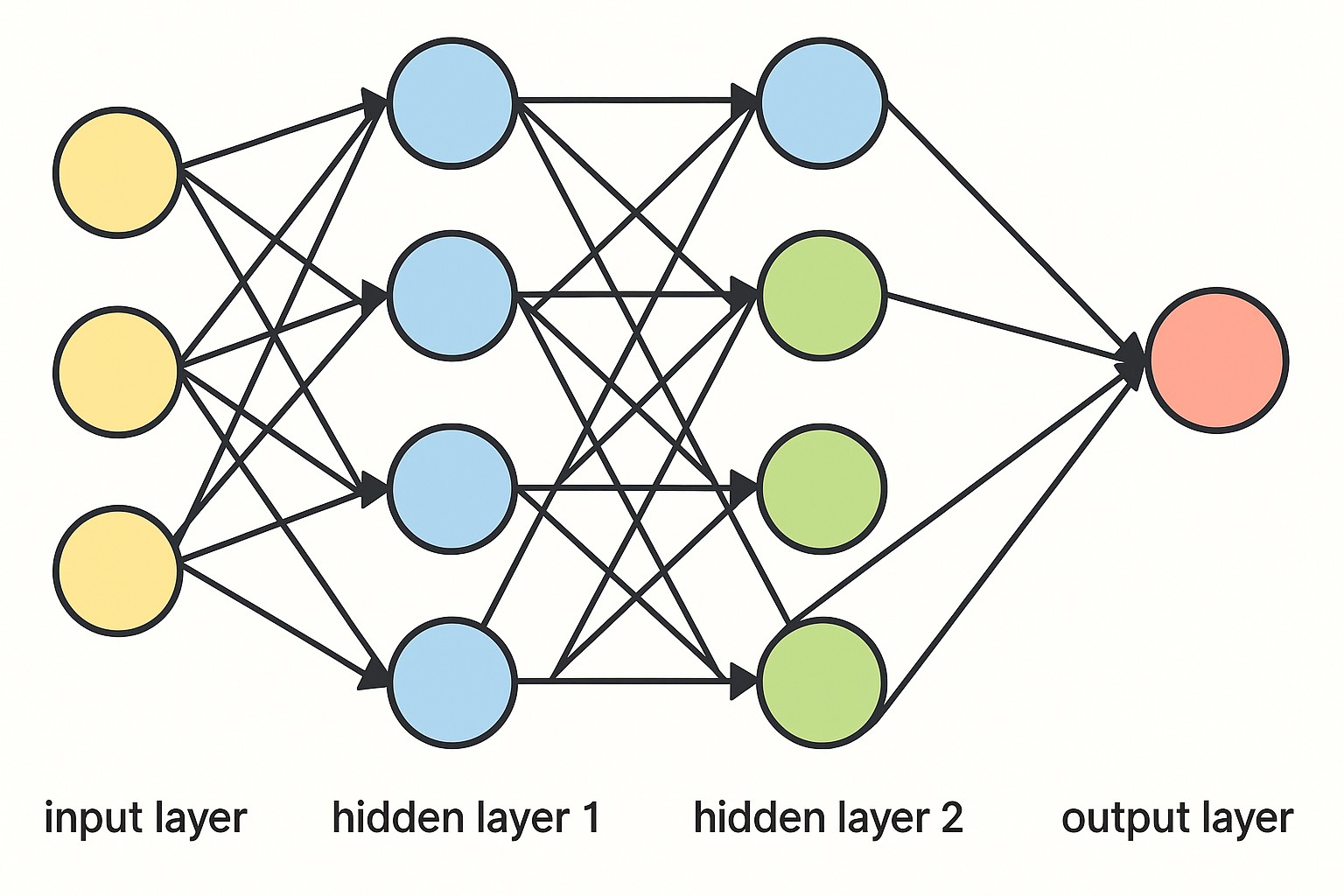
Before understanding how backpropagation works, it’s essential to understand what a neural network is and why it matters.

A neural network is a type of machine learning model inspired by how the human brain processes information. Instead of biological neurons, it uses artificial connections, simple mathematical units that are connected in layers. Each of these neurons receives inputs, processes them, and passes an output forward.

Neural networks are typically organized into three main parts:

• An input layer that takes in raw data,
• One or more hidden layers where patterns and features are extracted,
• And an output layer that produces the final prediction or decision.

Connections between these neurons carry weights, which determine how much influence one neuron has on another. Each neuron may also have a bias, a value that shifts the output up or down, adding flexibility to the learning process. When data moves from one layer to the next, through a series of weighted calculations and activation functions, it’s called the forward pass.

For a network to be useful, it needs to learn from mistakes by adjusting its internal settings to make better predictions over time. Backpropagation makes this possible. It works backward through the network, layer by layer, measuring how each weight and bias contributed to the final error. It then calculates how each one should be changed to reduce that error in the future.

To do this efficiently, backpropagation uses the chain rule to pass error signals backward from the output to the hidden layers. This is especially critical in multilayered networks, where the hidden layers can’t directly see the correct output.

How Backpropagation Works

Backpropagation works in a cycle of prediction and correction, happening in two main steps, a forward pass to make a prediction, and a backward pass to learn from the error.

The Forward Pass

First, data is fed into the network, and each neuron in a layer performs two basic functions by taking inputs from the previous layer and computing a weighted sum of its inputs, including a bias term. It then passes through an activation function to introduce non-linearity and produce the output for the next layer. This happens one layer at a time, starting from the input layer and moving forward through the hidden layers to the output and produces a prediction.

At this stage, the network hasn’t learned yet, it’s simply using its current settings to generate an output. But during this forward pass, it also stores key values like activations and weighted sums, which are reused in the learning phase that follows.

Calculating the Error

At the end of the forward pass, the network produces a prediction based on its current internal settings. This prediction is then compared to the correct output using a loss function, like mean squared error (MSE) for regression or cross-entropy for classification. The loss function calculates how far the prediction is from the target, producing a single error value. This error acts as the signal that guides how the network should adjust itself to improve in future training steps.

Backward Pass

In the backward pass, the algorithm moves from the output layer back to the input, tracing how each weight and bias contributed to the error. Since a neural network is made up of layers of functions, each building on the last, backpropagation uses the chain rule to break this down, computing how changes in one layer affect the final result.

The algorithm calculates gradients, which are just derivatives that tell us how much each weight and bias should change to reduce the error. For the output layer, this gradient comes from the difference between the predicted and actual values, scaled by the derivative of the activation function. In the hidden layers, the error is passed backward, and each neuron’s influence is measured based on how much it affected the layer that follows.

To adjust the network, backpropagation uses delta values (δ) to track how much each neuron contributed to the final error. These values are computed layer by layer from output to input and are used to calculate gradients. Along with the chain rule, they guide how each weight and bias should be updated, allowing the network to learn and improve with every example.

Updating the parameters

Once all gradients are computed, the network uses them to update its weights and biases. This is done through gradient descent, an optimization method that adjusts each parameter in the direction that lowers the loss. The size of each step is controlled by the learning rate, a setting that decides how fast or slow the model learns. If the learning rate is too high, the model may overshoot the optimal solution, and if it’s too low, learning can be slow or stuck.

This update phase completes one cycle of learning. The same process is repeated for many examples, often organized in batches, and repeated across multiple epochs (full passes through the training dataset), gradually learning the patterns in the data.

Conclusion

Backpropagation is a core concept in neural networks and a key reason these systems can learn from data and improve over time. This ability to adjust and refine internal parameters is what makes neural networks so powerful and so central to many advances in artificial intelligence AI.

Like any technique, it comes with limitations. Training can be slow, gradients may vanish or explode in deeper networks, and results often depend on high-quality data. It also lacks the continuous learning abilities seen in biological systems, and selecting the right architecture still involves trial and error.

Even so, with better tools, techniques, and computing power, many of these limitations can be managed. Backpropagation remains one of the most important building blocks in machine learning, and continues to shape the progress of AI today.