What is Vector Space Model?

The Vector Space Model (VSM) is a foundational representation framework in information retrieval and natural language processing. It exists to translate unstructured linguistic input into structured numerical form, enabling machines to compute relevance, similarity, and meaning using vector operations. As a representation model, VSM abstracts documents and queries into points in a multi-dimensional term space, where each dimension corresponds to a unique term from the corpus. This transformation allows algorithms to operate over text using algebraic principles, such as dot products and angle-based similarity.

The need for VSM emerged from the challenge of automating search, classification, and recommendation in large text collections. Human language is ambiguous, inconsistent, and syntactically diverse; without a formal numerical structure, it cannot be efficiently indexed or compared by computational systems. VSM solves this by imposing a fixed-dimensional structure on textual data, where meaning is approximated through patterns of term occurrence and co-occurrence. This makes it not just a method for retrieval, but a general-purpose foundation for many early and enduring NLP workflows.

Despite the rise of context-aware embeddings and neural language models, VSM remains relevant where transparency, interpretability, and implementation simplicity are priorities. Its vector structure makes it possible to trace retrieval decisions to specific term weights, an advantage in applications requiring auditability or real-time efficiency. As a baseline, it continues to offer a robust point of comparison for evaluating newer semantic models. For large-scale, low-complexity environments, such as regulatory systems, education platforms, or internal document search, VSM’s clarity and computational economy still make it a preferred choice.

Core Components and Functional Mechanism of the Vector Space Model

The Vector Space Model functions by reformatting natural language into high-dimensional vector representations that preserve term-level structure while enabling efficient similarity computation. This transformation allows text data, both documents and queries, to be encoded, compared, and ranked numerically.

Core components

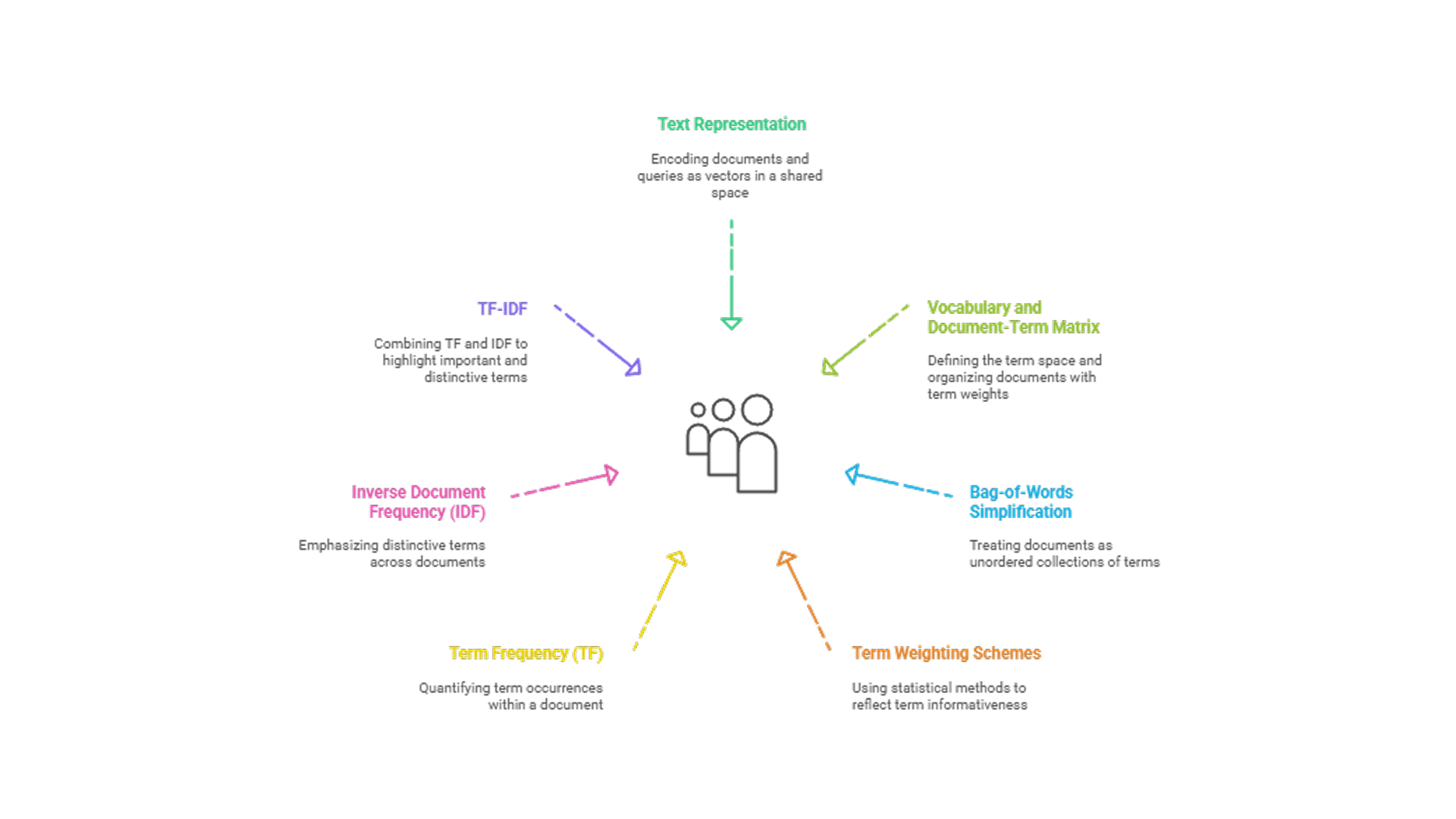
Text representation as vectors involves encoding each document and query within a shared high-dimensional space, where every axis corresponds to a unique term from the corpus vocabulary and the vector’s values reflect term importance within that document.

Vocabulary and document-term matrix define the structural foundation, with the vocabulary specifying the term space and the matrix organizing documents as rows and terms as columns, populated by numerical weights that capture each term’s contribution.

Bag-of-Words simplification frames documents as unordered collections of terms, enabling computational efficiency and scalability while sacrificing syntactic and contextual nuance due to the loss of word order.

Term weighting schemes: To reflect the relative informativeness of terms, VSM relies on statistical weighting schemes. These weights determine a document’s position in vector space, affecting how it is compared to other documents or queries.

• Term Frequency (TF) quantifies how often a term appears within a document and is often normalized to prevent longer documents from disproportionately influencing relevance calculations.
• Inverse Document Frequency (IDF) reduces the impact of terms that appear frequently across many documents, thereby emphasizing words that offer higher discriminative value.
• TF-IDF combines both frequency and rarity by multiplying TF and IDF, allowing the model to assign higher weight to terms that are both important within a document and distinctive across the corpus.

Interpretability and structure are enhanced by VSM’s reliance on explicit term weights and sparse matrix representations, enabling transparency, explainability, and ease of diagnostic inspection.

How the vector space model works

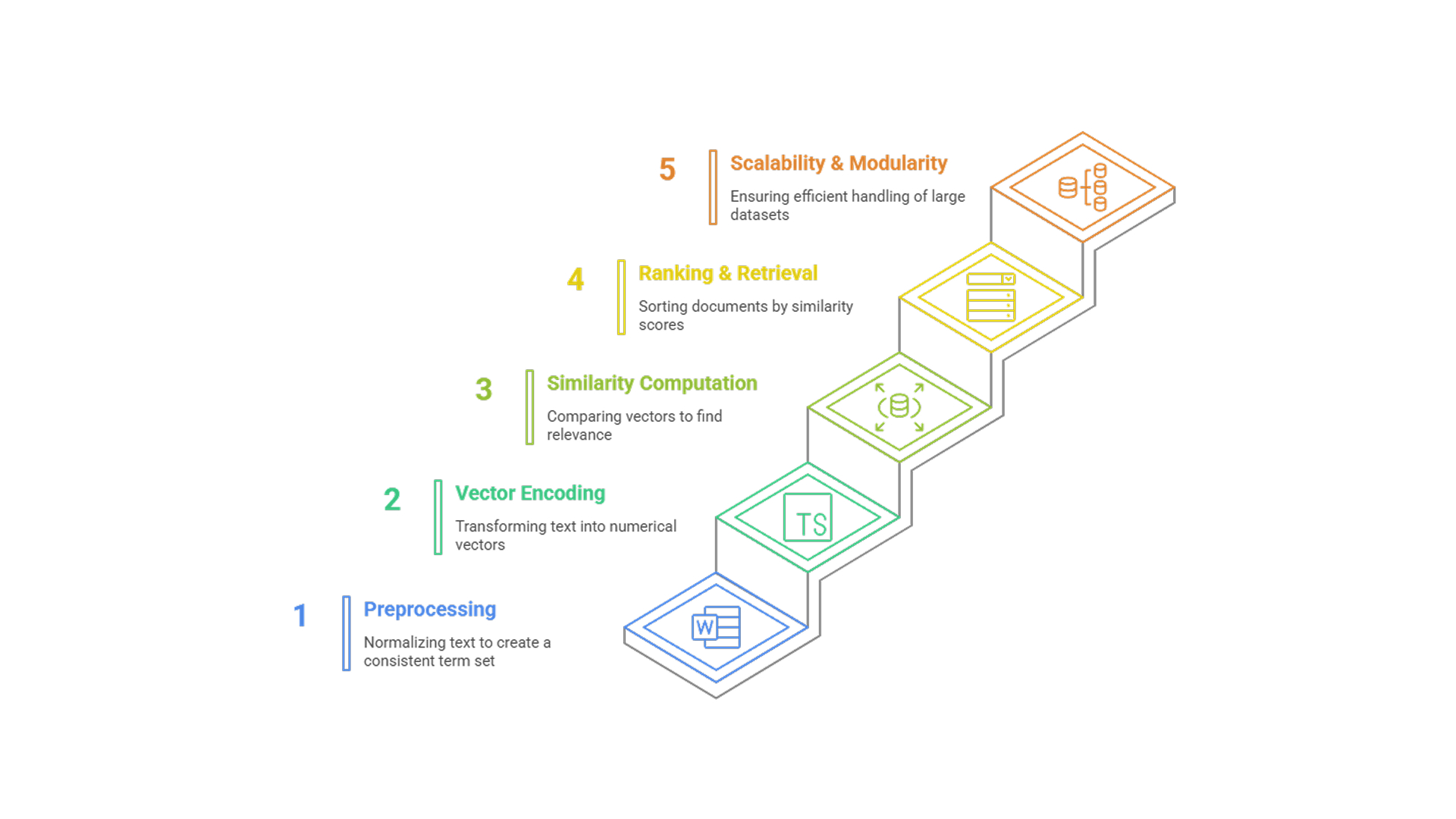
Preprocessing and vocabulary formation begin with standard linguistic normalization, including tokenization, lowercasing, removal of stop words, and stemming or lemmatization. This step produces a cleaned and consistent term set that forms the basis for constructing the model’s vocabulary.

Vector encoding of documents and queries transforms preprocessed text into fixed-length numerical vectors. Each vector aligns with the established vocabulary, with individual dimensions weighted according to term importance, typically through TF, IDF, or TF-IDF.

Similarity computation lies at the heart of VSM’s retrieval functionality. Documents and queries, once vectorized, are compared using cosine similarity, which quantifies the angle between their vectors in high-dimensional space. Cosine similarity is length-invariant and particularly effective for sparse representations, making it the preferred metric.

Ranking and retrieval is performed by sorting documents based on their similarity scores relative to the query vector. This enables relevance to be treated as a continuous scale, supporting retrieval even when there is partial term overlap between query and document.

Scalability and modularity are achieved through a streamlined, algebraic architecture. Each stage from text normalization to ranking is separable and efficient, with sparse matrix techniques allowing VSM to scale across large document collections in both academic and production pipelines.

Advantages of Vector Space Model

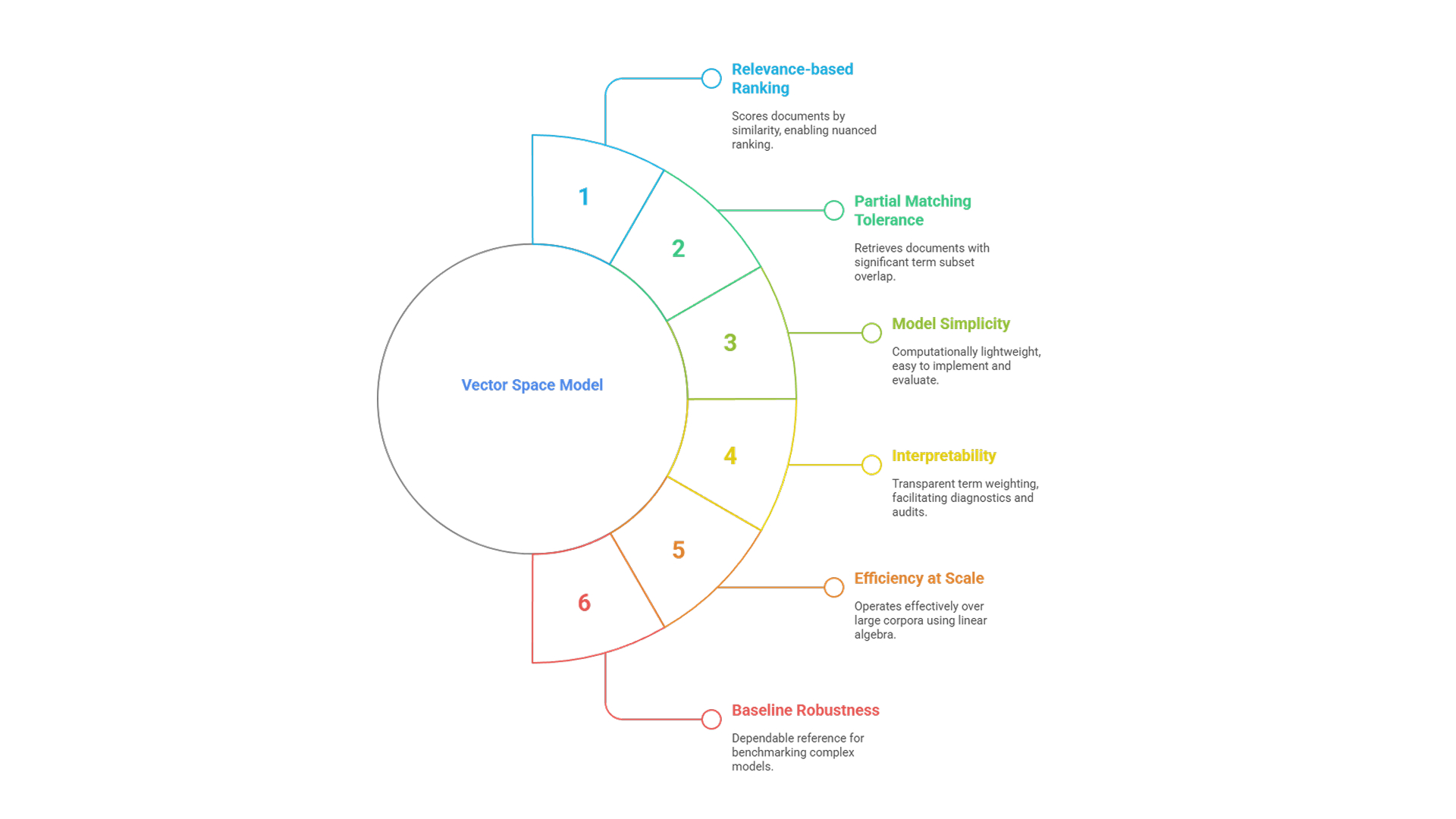
• Relevance-based ranking allows VSM to go beyond binary retrieval by scoring documents based on their similarity to a query. This graded approach supports nuanced ranking and retrieval even when there is only partial term overlap.
• Partial matching tolerance arises from its continuous similarity metric, typically cosine similarity, permitting retrieval of documents that do not contain all query terms but share a significant subset.
• Model simplicity ensures that VSM is computationally lightweight and easy to implement, making it accessible for baseline evaluations and practical applications where resources are constrained.
• Interpretability is achieved through transparent term weighting schemes and explicit vector representations, facilitating model diagnostics, audits, and regulatory explainability.
• Efficiency at scale stems from its reliance on linear algebra and sparse matrix operations, which allow it to operate effectively over large corpora.
• Baseline robustness positions VSM as a dependable reference point for benchmarking more complex or opaque models in IR and NLP, particularly those prone to underfitting when constrained by limited data or overly rigid design.

Conclusion

The Vector Space Model remains a foundational tool in information retrieval and natural language processing due to its clarity, efficiency, and ability to transform text into a computationally accessible form. Its use of weighted term vectors enables transparent document ranking, effective partial matching, and scalable deployment in systems that prioritize interpretability.

However, VSM’s core assumptions of term independence, no word order, and limited semantic awareness constrain its expressiveness, leading to sparse, high-dimensional representations and shallow language understanding. Modern techniques such as dimensionality reduction, word embeddings, and transformer-based models, which are built on the attention mechanism, address these gaps by introducing context and semantic depth.